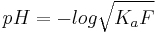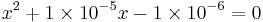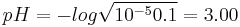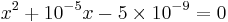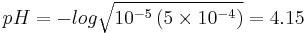Weak acid
Most acids are weak acids. A weak acid is an acid that dissociates incompletely. It does not release all of its hydrogens in a solution, donating only a partial amount of its protons to the solution. These acids have higher pKa than strong acids, which release all of their hydrogen atoms when dissolved in water. Examples of weak acids include acetic acid (CH3COOH) and oxalic acid (H2C2O4).
Contents |
Dissociation
Weak acids ionize in water solution to only a moderate extent; that is, if the acid was represented by the general formula HA, then in aqueous solution a significant amount of undissociated HA still remains. Weak acids in water dissociate as:
The strength of a weak acid is represented as either an equilibrium constant or as a percent dissociation. The equilibrium concentrations of reactants and products are related by the acid dissociation constant expression, (Ka):
The greater the value of Ka, the more the formation of H+ is favored, and the lower the pH of the solution. The Ka of weak acids varies between 1.8×10−16 and 55.5. Acids with a Ka less than 1.8×10−16 are weaker acids than water.
The other way to measure acid strength is to look at its percent dissociation, which is symbolized as α (alpha) and which can range from 0% < α < 100%. The percent dissociated is defined as
Unlike Ka, α is not constant and does depend on the [HA]. In general α will increase as [HA] decreases. Thus acids become stronger as they are diluted. If acids are polyprotic, then each proton will have a Ka. For example: H2CO3 + H2O → HCO3– + H3O+ has two Ka values because it has two acidic protons. The first Ka value is 4.46×10−7 (pKa1 = 6.351) and the second is 4.69×10−11 (pKa2 = 10.329).
Calculating the pH of a weak acid solution
The pH of a solution of a weak acid depends on the strength of the acid and the other components in the solution. In the simplest case, the weak acid is the only compound in water. In this case, the pH can be found from the concentration of the acid (symbolized as  ), from the
), from the 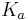 of the acid (symbolized as HA), and by solving for concentration of H+ (symbolized by x and represented more accurately as H3O+). Below is a table that organizes the information. On the first line, the reaction is written. On the second line, the initial conditions are written below each compound. Note that a value of water is not given because its term (activity) in the
of the acid (symbolized as HA), and by solving for concentration of H+ (symbolized by x and represented more accurately as H3O+). Below is a table that organizes the information. On the first line, the reaction is written. On the second line, the initial conditions are written below each compound. Note that a value of water is not given because its term (activity) in the 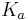 expression is technically equal to 1, but is often (conveniently) omitted. The third line shows how the value changes as the reaction goes to equilibrium. Then the last line gives the equilibrium concentrations and is simply the sum of each column.
expression is technically equal to 1, but is often (conveniently) omitted. The third line shows how the value changes as the reaction goes to equilibrium. Then the last line gives the equilibrium concentrations and is simply the sum of each column.
| HA(aq) | + | H2O(l) | → | A–(aq) | + | H3O+(aq) | |
| initial | F | — | 0 | 0 | |||
| change | -x | — | +x | +x | |||
| equilibrium | F - x | — | x | x |
Applying the equilibrium line to the 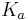 expression yields
expression yields
rearranging yields 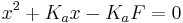 , which can be solved for x using the quadratic equation. The pH is then calculated as
, which can be solved for x using the quadratic equation. The pH is then calculated as 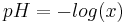 .
.
Simplification
However, if F is more than 1000× greater than Ka, then (1) the acid will not deprotonate much, (2) the value of x will be small, and therefore (3) F - x ≈ F. This simplifies the Ka expression to...
Solving for x yields
Then the pH = -log[H+]. The following equation then follows, but is only true if F >>> Ka
Comparison of the full and simplified methods
A certain weak acid has a Ka = 1×10−5 and the pH of two solutions needs to be found. One solution has a concentration of 0.10M and another has a concentration of 5×10−4M. The pH for both solutions will be calculated using both methods to yield 4 values, which will be compared.
0.1M Solution
The full method gives the following quadratic:
which gives x = 9.95×10−3 M and a pH = 3.00. The simplified method gives
So both methods yield the same result, but again F is more than 1000× greater than Ka. The next case does not have this condition and the results will differ.
5×10−4M Solution
The full method gives the following quadratic:
which gives x = 6.6×10−5 M and a pH = 4.18. The simplified method gives
Here, the results differ by 0.03 pH units. As F becomes closer in value to the Ka, then the difference will increase even more. However, in practice, it is rare to work with such dilute acids and the pH is also dependent on ionic strength and temperature. So in reality, the simplified method works well.
Conjugate acid/base pair
It is often stated that "the conjugate of a weak acid is a strong base". This statement can be misleading. Most weak acids that textbooks discuss have weak (not strong) conjugate bases. Truly, only the very weakest of acids have strong conjugate bases. For example, if a weak acid has a Ka = 10−5, then its conjugate base would have a Kb = 10−9 (from the relationship Ka × Kb = 10−14), which certainly is not a strong base. A very weak acid with a Ka = 10−20 would indeed have a strong conjugate base.
Corrosivity
While strong acids are generally assumed to be the most corrosive, this is not always true. The carborane superacid (H(CHB11Cl11)), which is one million times stronger than sulfuric acid, is entirely non-corrosive, whereas the weak acid hydrofluoric acid (HF) is extremely corrosive and can dissolve, among other things, glass and all metals except iridium.
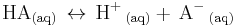
![\mathrm{ K_a\, =\, \frac {[H^%2B\,][A^-\,]}{[HA]} }](/2012-wikipedia_en_all_nopic_01_2012/I/e1160cb29e6e647fa04612aee2af4f35.png)
![\alpha = {{ \left[ A^- \right] } \over {\left[ A^- \right] %2B \left[ HA \right]}}](/2012-wikipedia_en_all_nopic_01_2012/I/2a02eca08939cca0b8b70efd4af2627a.png)
![K_a = { {[H^%2B][A^-]} \over {[HA]} } = {{x^2} \over {F - x}}](/2012-wikipedia_en_all_nopic_01_2012/I/388d5ea566217a7057d3b0ffee09e6ea.png)
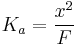
![x = \sqrt {K_a F}= \left[ H^%2B \right]](/2012-wikipedia_en_all_nopic_01_2012/I/8541f9b14f778e5d36ccdb72daf16dbe.png)